- Practical Cryptography for Developers
- 写给开发人员的实用密码学(一)—— 概览
- Project Wycheproof
- Cryptographic Best Practices
- The Physics of Brute Force
- Password Storage Cheat Sheet
- Bcrypt at 25: A Retrospective on Password Security
- 针对不安全加密问题的解决方法
- Tink Cryptographic Library
- Tink for Java HOW-TO
- Amazon Corretto Crypto Provider
- Use Fast Data Algorithms
开发人员应该对密码学有基本的了解,搞懂如何在编程语言中使用现代密码库,并从中挑选合适的算法,使用合适的 API 参数。盲目地从 Internet 复制/粘贴代码或遵循博客中的示例可能会导致安全问题 —— 曾经安全的代码、算法或者最佳实践,随着时间的推移也可能变得不再适用。
本文的目的是从实用角度出发,介绍一些现代密码学概念,给出就 2023 年而言的软件开发实践建议(以及不建议),帮助开发者在不必深入学习现代密码学的情况下写出安全的代码。由于当中涉及的知识过多,想要全部学习完并给出合适的实践建议实在是过于复杂,而当这一宏大工程完成后也许黄花菜都凉了,因此本文将在给出大纲的情况下缓慢更新(也许大纲也会调整),例如目前公钥密码系统相关的部分就相对而言更为含糊。
本文的大部分内容可以总结为如下路线图。读者应当牢记的是,如果本文在提到某个应用场景时使用了「XX 方案」这样的字眼(或者路线图中使用了 6 个以上字母),就代表开发者应当寻求 NaCl / Google Tink 这样的封装库,而不是自己用 BouncyCastle / OpenSSL 实现。
阐述原理涉及到过多的数学知识,很遗憾,笔者大学的时候这门课报名人数不足就没开班,因此这部分内容不会出现在本文中,有兴趣的读者可以自己深入研究。
随着时间的推移本文中的部分信息也可能发生变化。此外受限于笔者的知识水平,本文也可能出现一些错误,望读者斧正。
读者还应当清楚地意识到,维持系统安全性是一个整体的工程,有时候它不光是技术层面的问题,正如这个修改过的 XKCD 漫画所言:
消息编码
信息查询接口通过 URL 查询参数传输关键字,可以使用 URIEncode 或 Base64 进行编码,避免关键字中的一些字符无法被识别或错误转义。
但是记住消息编码不能帮你隐藏任何秘密,它只是保证了传输的信息不会因信息载体的描述能力有所损失。
标准的 Base64 编码结果不适合通过 URL 传输,因为 / 和 + 都会被 URIEncode。因此出现了适用于 URL 的 Base64 变种,使用 - 和 _。
// 使用 java.util.Base64
String encoded = Base64.getEncoder().encodeToString(source.getBytes(StandardCharsets.UTF_8));
String decoded = new String(Base64.getDecoder().decode(encoded));
// URL 适配的 Base64 编解码
String encoded = Base64.getUrlEncoder().encodeToString(source.getBytes(StandardCharsets.UTF_8));
String decoded = new String(Base64.getUrlDecoder().decode(encoded));
另一种方式是使用十六进制,例如 com.google.guava:guava 中的 com.google.common.io.BaseEncoding,不过一般的应用场景是以字符串模式处理字节数组。
BaseEncoding.base16().lowerCase().encode(hashed);
加密散列函数 / 加密哈希函数
散列函数可以把一段数据映射成一个固定长度的字符串,理想的散列函数应当满足:
- 快速
- 确定性:同样的输入总是产生同样的输出
- 雪崩效应: 的一小点变化将使 发生巨大变化
加密散列函数则额外具有如下特性:
- 抗碰撞:通过统计学方法(彩虹表)很难或几乎不可能猜出哈希值对应的原始数据
- 强无碰撞性:给定散列函数 ,无法找到 满足
- 弱无碰撞性:给定散列函数 以及 ,无法找到另一个 满足
- 不可逆:给定 ,无法推测出
SHA-2(SHA-224 / SHA-256 / SHA-384 / SHA-512)
SHA-2 是久经考验的行业标准,被广泛用于 HTTPS 协议、文件完整性校验、比特币区块链等各种场景,一般来说使用 SHA-256 就有不错的表现。
MessageDigest digest = MessageDigest.getInstance("SHA-256");
byte[] hashed = digest.digest(source.getBytes(StandardCharsets.UTF_8));
SHA-256 计算出的散列值长度为 256-bits,转换为字节数组的话有 16 位。只是用于存储的话,你不需要把它转换成别的格式,有「人类可读」需求的话可以转换为十六进制字符串。
一些系统使用了 hash(secret + message) 计算签名的方法实现消息认证(有关消息认证的知识后面还会再提到),这种方案容易受到长度扩展攻击。
长度拓展攻击(Length extension attack): 基于 Merkle–Damgård 结构的散列算法(MD5、SHA-1、SHA-2 等)在已知 的值以及 长度的情况下,可以推算出 的值,其中 为任意数据。
如果要做消息认证,考虑 SHA-3(或者 HMAC,后面会提到)。
其他选择
BLAKE2 是一系列快速、高度安全的加密散列函数,打进了 SHA-3 NIST competition 的决赛圈。当然这场比赛的胜者是 Keccak 算法,于是 SHA-3 就用这个算法实现了。SHA-3(SHA3-224,SHA3-256,SHA3-384,SHA3-512)在相同长度下有着比 SHA-2 更高的安全性,且不会受到长度拓展攻击。Keccak-256 则广泛应用于以太坊。
SHAKE-128 和 SHAKE-256 是 SHA3-256 和 SHA3-512 的变体,特点是可以改变输出的长度。
// 输出 160-bits 的哈希值
SHAKE-256('hello', 160) = 1234075ae4a1e77316cf2d8000974581a343b9eb
从安全角度考虑避免使用的散列算法
一些老一代的加密散列算法,如 MD5,SHA-1 被认为是不安全的,并且都存在已被发现的碰撞漏洞。只有在碰撞不会产生问题的情下才考虑使用(比如 Git 为 commit 产生标识符使用了 SHA-1),不过这时候通常会有更好的选择。
非加密散列函数
加密散列函数为了实现更高的安全性付出了计算复杂耗时长的代价,然而实际应用中很多场景不需要这么高的安全性,相反可能会对速度、随机均匀性等有更高的要求,这就催生出了很多非加密散列函数。
xxHash 支持生成 32 和 64 位的哈希值,性能非常猛,如果你的程序在这方面遇到了瓶颈,不妨考虑下。
MurmurHash 是另一种非加密型哈希函数,对于规律性较强的 key 有更好的随机分布表现,为 Redis、NGINX、Cassandra、HBase、Lucene 等软件采用。
密码学安全伪随机数生成器(Cryptography Secure Pseudo-Random Number Generators,CSPRNG)
满足如下两个特性即可称之为密码学安全随机数生成器:
- 能通过「下一比特测试」:即使获知了该 PRNG 的 k 位,也无法使用合理的资源预测第 k+1 位
- 如果攻击者猜出了 PRNG 的内部状态,或该状态因某种原因而泄漏,攻击者也无法重建出内部状态泄漏之前生成的所有随机数
编程语言中的 CSPRNG 有:
- Java:
java.security.SecureRandom - Python:
secrets库或者os.urandom() - JavaScript in Browser:
window.crypto.getRandomValues(Uint8Array) - JavaScript in Node:
crypto.randomBytes()
// 使用 java.security.SecureRandom
SecureRandom random = new SecureRandom();
byte[] bytes = new byte[20];
random.nextBytes(bytes);
System.out.println(BaseEncoding.base16().lowerCase().encode(bytes));
System.out.println(random.nextBoolean());
System.out.println(random.nextInt());
System.out.println(random.nextInt(10));
System.out.println(random.nextGaussian());
创建随机 ID、随机数、初始向量或者随便什么随机变量时,确保总是使用操作系统内核空间中的 CSPRNG,即 /dev/urandom,Java 开发者可以通过 new SecureRandom().getAlgorithm() 确认这一点。
密钥派生函数(Key Derivation Function,KDF)
密码学中的密钥(key)通常指的是一个大整数(或者说指定长度的二进制序列),而人类记住一个字符串格式的口令(password)要容易得多,这之间的转换需要用到密钥派生函数。
不要觉得记一个整数有什么难的,一个 256-bits 的 key 能够表示 0 到 1.15792089e77 间的任意一个整数。
由于一般人使用的密码不会超过 15 位,还会使用很多常见的组合(姓名、生日、部门、admin、p@ssword 等等),仅仅使用散列函数(或者「级联」散列函数,比如 SHA256(SHA256(SHA256(password))),别笑)作为 KDF 的话,通过统计学的方法碰撞出原文还是比较容易的。
在计算 hash 时加盐(salt)曾经是一种比较好的方法,不过现在攻击者使用 FPGA、ASIC 或者 GPU 也可以比较容易地暴力破解。
一个好的 KDF 主要从三个维度考虑提升碰撞难度:
- 增加时间复杂度,消耗更多的计算资源
- 增加空间复杂度,消耗更多内存空间
- 使用无法分解的算法,只允许单线程运算
密码存储
在网站登录功能中,我们需要比较用户提供的口令是否与数据库内的记录是否一致,由于我们不能直接存储用户密码(想做第二个 CSDN?),KDF 就可以派上用场。
将 {salt, KDF(password, salt)} 存储在数据库中。当数据库被攻破时,攻击者需要消耗更多的资源破译出原本的口令(不考虑其他防御措施,好的 KDF 可以耗去 0.2 秒的计算时间,拉低攻击的频率(或者大幅提高代价))。对于正常的用户登录流程,由于一段时间内只需要执行一次这种操作,这个策略是完全可接受的。
| Security | Adaptable Work Factor | Memory-hardness | Year Introduced | |
|---|---|---|---|---|
| CRYPT | Not recommended | No | No | 1970s |
| MD5crypt | Not recommended | No | No | 1994 |
| BCRYPT | High | Yes | No | 1999 |
| PBKDF2WithHmacSHA1 (RFC 2898, 2000) | Moderate to high | Yes | No | 2000 |
| Scrypt (Percival, 2013) | High | Yes | Yes | 2009 |
| Argon2 (Biryukov & Dinu, 2016) | High | Yes | Yes | 2015 |
目前来说有 2 个方案值得选择,表现最好的 Argon2 是 2015 年密码 Hash 竞赛的赢家,如果可以的话选择 Argon2id:
- Argon2
- SCrypt
当然除了使用 KDF,在用户连续登录失败 2-3 次后临时锁定帐户或增加验证也是必要的,在数据的传输过程中也要使用 TLS。
在 Java 应用中使用
如果你使用 Spring Security 来管理用户密码的话,不需要考虑这个问题。否则可以阅读 org.springframework.security:spring-security-crypto 较新版本的包中 org.springframework.security.crypto 下的代码以了解怎样正确地配置这些 KDF(推荐参数会随着安全形势变化更新)。
Argon2 和 SCrypt 依赖 org.bouncycastle:bcprov:
// org.springframework.security.crypto.argon2.Argon2PasswordEncoder
Argon2PasswordEncoder(int saltLength, int hashLength, int parallelism, int memory, int iterations)
- saltLength: the salt length (in bytes)
- hashLength: the hash length (in bytes)
- parallelism: the parallelism
- memory: the memory cost
- iterations – the number of iterations
// org.springframework.security.crypto.scrypt.SCryptPasswordEncoder
SCryptPasswordEncoder(int saltLength, int hashLength, int parallelism, int memory, int iterations)
- cpuCost: cpu cost of the algorithm (as defined in scrypt this is N). must be power of 2 greater than 1
- memoryCost: memory cost of the algorithm (as defined in scrypt this is r)
- parallelization: the parallelization of the algorithm (as defined in scrypt this is p)
- keyLength: key length for the algorithm (as defined in scrypt this is dkLen)
- saltLength: salt length (as defined in scrypt this is the length of S)
如果你使用了 Spring Security,可能会发现 Spring 在编码用户密码使用了 BCrypt 算法,虽然总的来说 BCrypt 不如 Argon2id 和 SCrypt 来的有效,但我们事前也提到过许多参数若是配得不对,效果就会大打折扣。所以除非你打算换成 Argon2,否则最好让它留在原来的位子上。
org.springframework.security.crypto.bcrypt.BCryptPasswordEncoder 使用了 Spring 自己实现的 BCrypt 算法,只有一个 strength 参数需要调整,可选 4-31 范围内的整数,默认构造函数目前使用了 10(org.springframework.security:spring-security-crypto:6.0.3 中)。
许多框架和库的实现最终会输出一个包含了算法配置、盐和散列值的字符串,以加密 admin 这个「口令」为例:
# Argon2id
$argon2id$v=19$m=16384,t=2,p=1$YQlURhTwe8pHnvMlEwYqrg$NYEq5pW6gAKvGMknwjsvBTeYKJ6s6E9vBaKKVO4Elow
# Scrypt
$100801$p03RqYIPB7nQ35hIzudydw==$BM1thGRnj+mkcWPzC1uxzaUePV6JLF67IDPR6kH0hgI=
# Bcrypt
$2a$10$w1af/ThE5.wc8JHgk9qzieIOuLv.b7HXuoTbvGDer8CTpY011X1ha
不推荐列表
之前普遍使用的 PBKDF2 通过多次迭代和 Padding 来消耗 CPU 资源,缺乏对 GPU、ASIC、FPGA 的免疫能力,正在不可避免地滑向「不应当使用」列表。如果你只能使用这一方案,根据开放式 Web 应用程序安全项目(OWASP)在 2021 年的建议,对 PBKDF2-HMAC-SHA256 使用 310000 次迭代。当然了,他们似乎每两年就把推荐的迭代次数翻一番,2023 年更新本文时我又去 看了下,已经变成「use PBKDF2 with a work factor of 600,000 or more and set with an internal hash function of HMAC-SHA-256」了。
此外应当避免使用:
- SHA-2,SHA-1,MD5(甭管什么安全的不安全的散列函数以及它们的组合和级联)
- 自己造的轮子(除非你是一位数学家)
- 任意一种加密算法
消息鉴别码(Message Authentication Code,MAC)
MAC 通过检测消息内容的更改来证实消息的完整性与真实性。
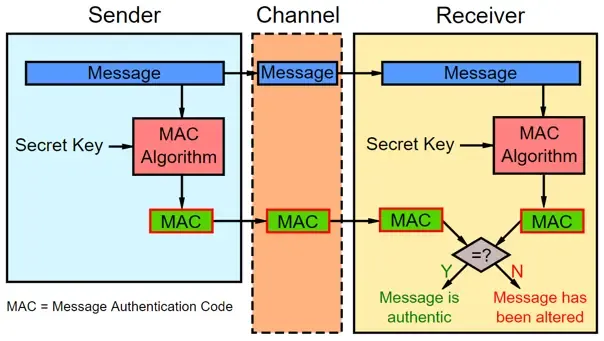
应仅将 MAC 用于消息身份验证,而不应将其用于生成伪随机字节等其他目的。
在 MAC 的应用场景中,双方使用预先共享的相同密钥(pre-shared key),这是 MAC 与数字签名的主要区别之一。
Hash-based Message Authentication Code, HMAC
当我们使用散列函数来计算 MAC 时,比较流行的方案有 HMAC(Hash-based MAC,例如 HMAC-SHA256)和 KMAC(Keccak-based MAC)。
HMAC 的实现大致可表示为 hash(secret + hash(secret + message)),因此不受长度扩展攻击影响。
动态口令(One-Time Passwords, OTP)
动态口令是每隔一定的时间间隔生成的不可预测随机数字组合。由于有效期较短,不容易受到重放攻击。通常网银、网游的密保、两步验证 APP 都是 OTP 的应用场景。
双方约定一个密钥,然后计算一些数据的 HMAC,通过某种方法转换成数字组合进行比对,称为 HOTP(HMAC-based One-time Password)。有一些方案使用计数器作为「一些数据」,就是 COTP(Counter-based One-Time Password),不过服务器端和客户端丢失同步状态的时候比较麻烦,所以另一个基于时间戳的 TOTP(Time-based One-Time Password)方案看起来就很不错了,计算方式为 OTP(K, T) = Truncate(HMAC-SHA1(K, T)),其中 T 根据当前 Unix 时间戳得出。
使用 TOTP 需要注意给定充足的时间窗口,让用户在这个时间段内输入的 OTP 保持不变,一般为 30 秒。为了防止服务器与客户端时间不同步导致校验失败,验证时可能也会计算前一个和后一个时间窗口的 TOTP。
由于遍历 6 个数字还是比较简单的,需要在一定错误尝试之后限制用户行为。
如果站点通过 OTP 实现两步验证,那么在开启该项配置时通常会要求用户保存一些「救援代码」,这些救援代码也是一次性的,目的是允许用户临时脱离 OTP 设备(例如丢失设备)也能验证身份。这些「救援代码」可以经 KDF 处理后存储在数据库中。
如果你打算在 Java 项目中使用 TOTP,那么笔者提供了一个实现,你可以从 Maven 中央仓库以 cc.ddrpa.security:totp 找到。
对称加密
对称密钥加密算法使用一个共享密钥来加密和解密消息。
即使计算机进入量子时代,仍然可以沿用当前的对称密码算法。因为大多数现代对称密钥密码算法都是抗量子的(quantum-resistant),这意味当使用长度足够的密钥时,强大的量子计算机无法破坏其安全性。目前来看 256 位的 AES 在很长一段时间内都将是量子安全的。
单纯使用加密算法是不够的,这是因为有的加密算法只能按块进行加密,而且通常加密算法不保证密文的真实性、完整性。因此现实中我们通常会把对称加密算法和其他算法组成「加密方案」。
一个「分组加密方案」通常包括:
- 分组密码工作模式(用于将分组密码转换为流密码,有 CBC / CTR 等)+ 消息填充算法(如 PKCS7):分组密码算法需要借助这两种算法才能加密任意大小的数据
- 分组密码算法(如 AES):使用密钥安全地加密固定长度的数据块
- 消息认证算法(如 HMAC):用于验证消息的真实性、完整性、不可否认性
流密码加密方案本身就能加密任意长度的数据,因此不需要「分组密码工作模式」与「消息填充算法」。
分组密码工作模式
CTR(计数器)模式在大多数情况下是一个不错的选择,因为它具有很强的安全性和并行处理能力,但它不能提供身份验证和完整性校验。使用伽罗华域(Galois Field,有限域)乘法运算计算消息的 MAC 值的方法称为 GMAC,配合 CTR 诞生了 GCM(伽罗瓦/计数器,Galois / Counter)模式。
GCM、CTR 和其他分组模式会泄漏原始消息的长度,因为它们生成的密文长度与明文消息的长度相同。如果你想避免泄露原始明文长度,可以在加密前向明文添加一些随机字节并在解密后将其删除。
其他的分组在某些情况下可能会有所帮助,但很可能有安全隐患。除非你很清楚自己在做什么,否则应当始终选择这两个分组模式。
不要使用 EBC(电子密码本)模式,这种模式使用相同的密钥对明文分组单独加密。
CBC(密文分组链接)模式中加密算法的输入是上一个密文组与本明文分组的异或。虽然 CBC 模式通常被认为是安全的并被广泛应用,在某些情况下,CBC 阻塞模式可能容易受到「Padding Oracle」攻击
密文填塞攻击,Padding Oracle attack 在对称加密中,填充神谕攻击可应用在分组密码工作模式上,其反馈的“神谕”(通常为服务器)信息将返回泄漏密文填充的正确与否。攻击者可在没有加密密钥的情况下,透过此信息的神谕密钥解密(或加密)信息。
初始向量(Initialization Vector,IV)/ Nonce / Salt
通过添加不可预测的随机数可以使同样的明文产生不同的密文,从而确保密文的不可预测性。
在 CBC 等模式中,初始向量在第一个分组的加密过程中代替「上一个密文组」,此时 IV 的大小应与密码块大小相同,例如 AES 的密码块是 128 位,那么 IV 也是 128 位。
CTR 模式也使用 128-bits 的初始向量。
在 GCM 模式中,初始向量也被称为 Nonce,用于影响计数器。应当使用 96-bits 的随机数。
IV / Nonce / Salt 必须唯一且不可预测,但不必保密。开发者应使用 CSPRNG 生成随机变量并与密文一起存储或传输。常见错误是使用相同的密钥和随机变量加密多条消息,这使得针对大多数分组模式的各种攻击成为可能。
分组密码算法 AES
AES 被证明是高度安全、快速且标准化的,到目前为止没有发现任何明显的弱点或攻击手段,而且几乎在所有平台上都得到了很好的支持。
AES 使用 128-bits 大小的分组,密钥的长度则任意,一般为 128-bits、192-bits 或 256-bits。大部分场景下 AES-128(128-bits)已经足够,如果对安全有更高要求的话则推荐使用 AES-256(256-bits)。
AES 通常与 CTR / GCM 分组模式组合成分组加密方案(AES-CTR 或 AES-GCM)以处理流数据。
认证加密(Authenticated Encryption,AE)与带有关联数据的认证加密(Authenticated Encryption with Associated Data,AEAD)
AES 并不保证密文的真实性、完整性,也就是说加密一段文字,修改密文,解密,还是能得到一段文本。那么,我们要如何确认对方接收到的加密信息在解密后与原文保持一致?
可以使用 MAC,接收方计算解密信息的 MAC 并与接收到的值比较。
这种方案称为认证加密。AES-256-CTR-HMAC-SHA256 就表示使用 AES-256 与 Counter 分组模式进行加密,使用 HMAC-SHA256 进行消息认证。另一些认证加密算法如 AES-GCM 和 ChaCha20-Poly1305 则内置了校验计算。
带有关联数据的认证加密(AEAD)是认证加密的更安全变体。AEAD 将不需要加密的关联数据(AD)与密码文本和它应该出现的上下文结合在一起。因此试图将有效的密码文本「剪切粘贴」到不同的上下文中的行为可以被检测和拒绝,确保整个数据流得到验证和完整性保护。
这么说似乎有点抽象,举个例子,假设我们的医疗系统支持用户查看自己的病历(SELECT encrypted-medical-history FROM table WHERE user-id = $current_user),攻击者在能够修改数据库的情况下,只需要把自己的 encrypted-medical-history 属性替换为其他用户的数据,就能以合法途径解密所有数据。
如果我们把 user-id 作为加 / 解密上下文,至少可以阻止这类攻击。
另一个用法是使用当前日期作为上下文,这样光凭密文而不知道加密日期是无法正确解密的,在一定程度上实现了有时效性的加密。
其他知识
- 纯软件实现的话,ChaCha20-Poly1305 比 AES-GCM 要快
- 硬件加速加持的 AES-GCM 比 ChaCha20-Poly1305 快
- AES-CTR HMAC 的软件实现比 AES-GCM 快
- 实现安全的 Poly1305 比 GCM 要容易些
- AES-GCM 是行业标准
在应用中应用 AEAD 方案
使用 javax.crypto.Cipher 实现 AEAD
以 AES128-GCM-NoPadding 为例:
// 通常情况下 key 应当秘密地获取
// 或是通过 Argon2 等 KDF 从口令(和其他参数)生成
byte[] key = generateRandomBytes(128);
// iv 不需要加密,且应当随 cipher text 一起存储
// AES/GCM 使用 96-bits 的 nonce
byte[] iv = generateRandomBytes(96);
byte[] plainText = "Hello World!".getBytes(StandardCharsets.UTF_8);
// 加密
Cipher cipher = Cipher.getInstance("AES/GCM/NoPadding");
// Tag(其实就是 MAC)长度为 128-bits
cipher.init(Cipher.ENCRYPT_MODE, new SecretKeySpec(key, "AES"), new GCMParameterSpec(128, iv));
// 添加上下文信息
// 有些环境不支持空的 AAD,例如 Android KitKat (API level 19)
cipher.updateAAD(new byte[0]);
// 密文的长度应当等于明文长度 + Tag 长度
byte[] cipherText = cipher.doFinal(plainText);
// 解密
cipher = Cipher.getInstance("AES/GCM/NoPadding");
cipher.init(Cipher.DECRYPT_MODE, new SecretKeySpec(key, "AES"), new GCMParameterSpec(128, iv));
cipher.updateAAD(new byte[0]);
byte[] decryptedText = cipher.doFinal(cipherText);
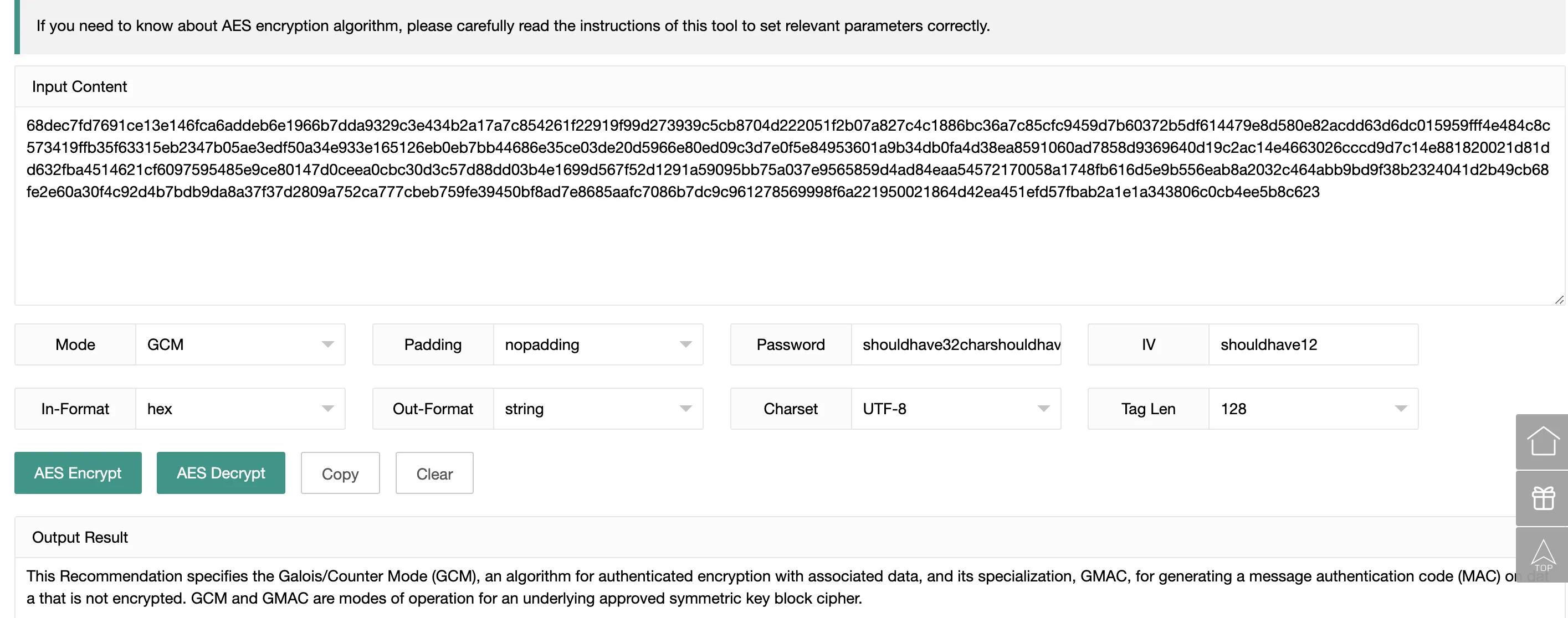
许多在线 AES 工具既没有提供初始向量的输入方法,也没有明确指出把用户口令转换为密钥的 KDF,更不要说使用 AAD 了。由于参数的不同,通过这些工具加密的内容可能到了另一些工具那里却无法解密。笔者推荐使用 AES Encryption and Decryption 这个工具来做验证。
当然为了让这个工具可以正确接收密钥和 IV,特别构造了对应的字符串。
使用 Google Tink
AEAD 方案已经非常简单了,尽管如此你还要记住 128 / 96 这些参数,在发送加密结果时还要记住一起发送 IV。因此笔者给出的建议是 —— 别自己弄,你应该使用 NaCl / Google Tink 这样的加密库。
// Register all AEAD key types with the Tink runtime
AeadConfig.register();
// Read the keyset into a KeysetHandle
keysetHandle = CleartextKeysetHandle.read(
JsonKeysetReader.withInputStream(
this.getClass().getClassLoader()
.getResourceAsStream("tinkey-keyset")));
// Get the primitive
Aead aead = keysetHandle.getPrimitive(Aead.class);
byte[] ciphertext = aead.encrypt(plaintext, associatedData);
没有任何参数配置,你会得到 012491689977a2359f0f5d1e52a4b8da2ab05a595874f430a845f22f7e6ee2f5f20b4b1a7824c5a436374ce2d11a,这就是解密需要的全部了(当然还有密钥和 AAD)。
如果消息的接收方能够使用 Google Tink,那最好,否则就需要按照 Tink 的格式解析密文再进行解密。
以最简单的 AES128-GCM 为例,分析 Tink 的代码可以写出直接调用 javax.crypto.Cipher 的解密过程。
首先把 Tink 的加密结果恢复为字节数组,有些信息是提供给 Tink 的,可以丢弃。
byte[] cipherText = BaseEncoding.base16().lowerCase().decode("012491689977a2359f0f5d1e52a4b8da2ab05a595874f430a845f22f7e6ee2f5f20b4b1a7824c5a436374ce2d11a");
// 第一个字节表示版本号
assertEquals(0x01, cipherText[0]);
// 接下来 4 字节转换成 Long 类型,是密钥在密钥集中的 ID
assertEquals(613509273L, Longs.fromBytes((byte) 0, (byte) 0, (byte) 0, (byte) 0, cipherText[1], cipherText[2], cipherText[3], cipherText[4]));
AES/GCM 使用 12 字节长的 nonce 和 16 字节长的 tag,密文长度则与明文长度相同。
// 12-byte nonce
byte[] nonce = new byte[12];
System.arraycopy(cipherText, 5, nonce, 0, 12);
// 13-byte ciphertext same as plain text with 16-byte tag (or mac)
byte[] cipherTextWithTag = new byte[13 + 16];
System.arraycopy(cipherText, 17, cipherTextWithTag, 0, 29);
可以自己用 javax.crypto.Cipher 实现解密:
Cipher cipher = Cipher.getInstance("AES/GCM/NoPadding");
cipher.init(Cipher.DECRYPT_MODE, new SecretKeySpec(key, "AES"), new GCMParameterSpec(128, nonce));
cipher.updateAAD(associatedData);
byte[] decrypted = cipher.doFinal(cipherTextWithTag);
通过 com.google.crypto.tink.subtle.AesGcmJce 也可以在不使用密钥集等概念的情况下享受 Tink 的大部分好处:
AesGcmJce aesGcmJce = new AesGcmJce(key);
byte[] cipherText = aesGcmJce.encrypt(PLAIN_TEXT.getBytes(StandardCharsets.UTF_8), associatedData);
// 密文长度等于 iv 长度 + 明文长度 + tag 长度
assertEquals(12 + PLAIN_TEXT.getBytes(StandardCharsets.UTF_8).length + 16, cipherText.length);